The unit circle is a fundamental concept in trigonometry and mathematics, serving as a cornerstone for understanding angles, radians, and trigonometric functions. Whether you’re a high school student gearing up for IB exams or a college student diving into calculus, mastering the this topic can make your mathematical journey significantly smoother. In this comprehensive guide, we’ll break down the unit circle into digestible parts, provide unique insights, and equip you with a cheat sheet to succeed.
What Is the Unit Circle?
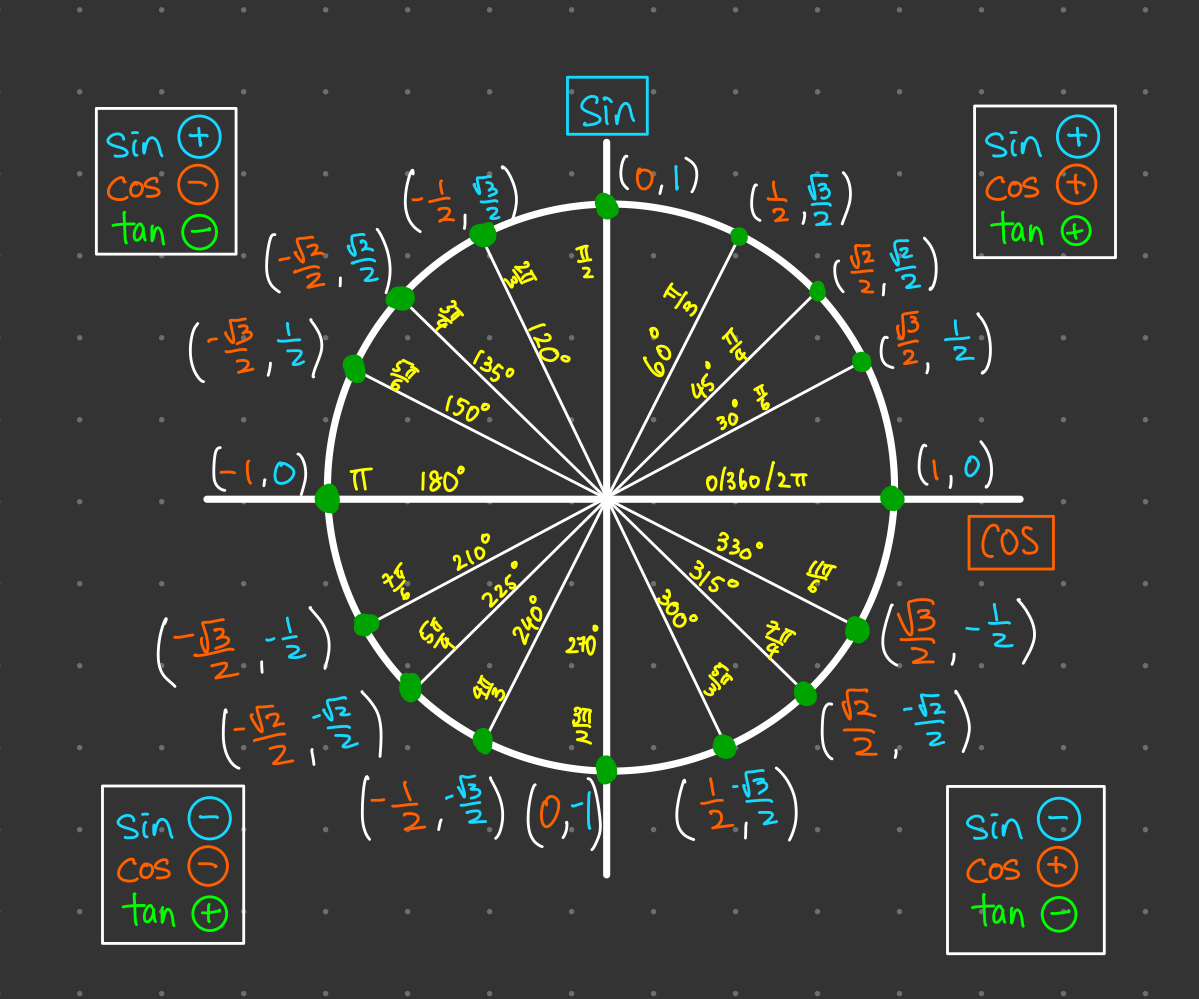
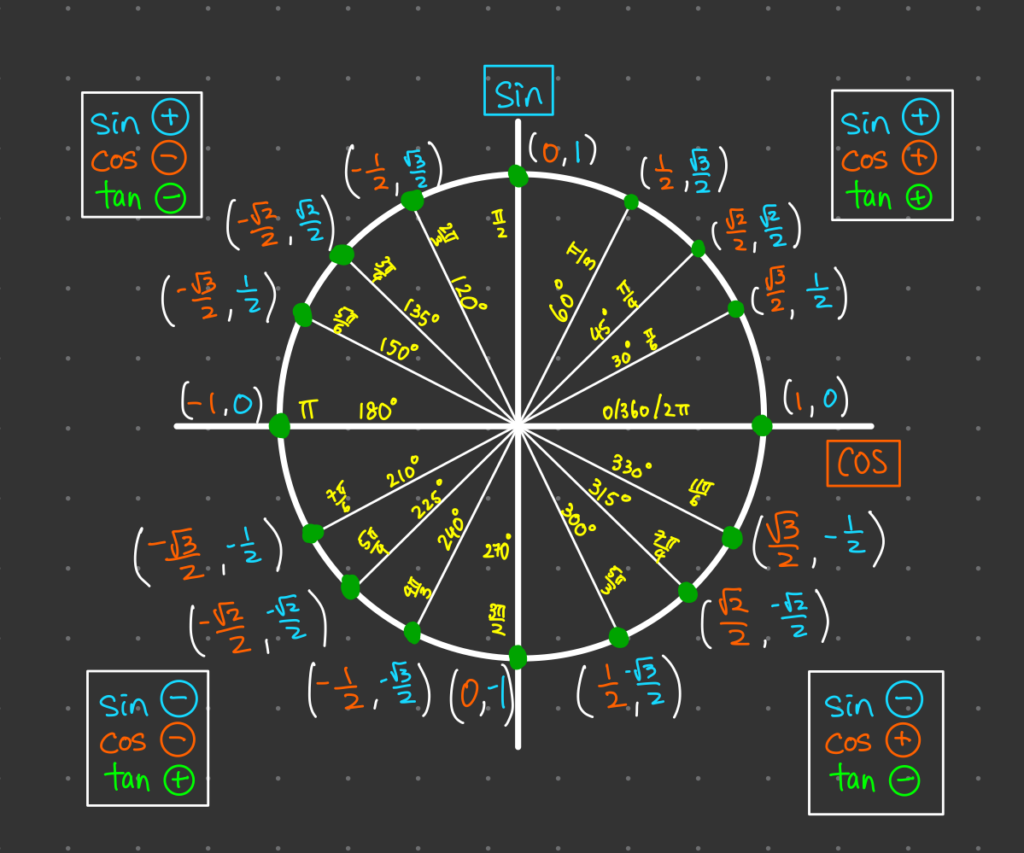
The unit circle is a circle with a radius of 1, centered at the origin (0, 0) on a coordinate plane. Its simplicity is deceptive because it provides the foundation for understanding trigonometric functions, angles, and their relationships.
In essence:
- Radius: 1 unit
- Center: Origin (0, 0)
- Equation: x^2 + y^2 = 1
This simple structure allows us to define the sine, cosine, and tangent of any angle using the coordinates of points on the circle.
Why Learn the Unit Circle?
The unit circle is not just a theoretical concept; it has practical applications in:
- Trigonometry: Understanding sine, cosine, and tangent.
- Physics: Modeling waveforms like sound and light waves.
- Engineering: Designing circuits, bridges, and other systems.
- Computer Graphics: Rotating objects and simulating natural phenomena.
Key Benefits
- Memorization Shortcut: Once you understand the circle, you can recall trigonometric values without relying on calculators.
- Simplifies Complex Concepts: The unit circle lays the groundwork for topics like Fourier transforms and polar coordinates.
Structure of the Unit Circle
Quadrants and Angles
The unit circle is divided into four quadrants:
- Quadrant I: Angles between 0^{\circ} and 90^{\circ}
- Quadrant II: Angles between 90^{\circ} and 180^{\circ}
- Quadrant III: Angles between 180^{\circ} and 270^{\circ}
- Quadrant IV: Angles between 270^{\circ} and 360^{\circ}
Key Points on the Circle
Certain angles, measured in degrees or radians, correspond to specific points on the unit circle. Here are the most important ones:
| Angle (\theta) | Radians | Coordinates ((x, y)) |
|---|---|---|
| 0^{\circ} | 0 | (1, 0) |
| 90^{\circ} | \frac{\pi}{2} | (0, 1) |
| 180^{\circ} | \pi | (-1, 0) |
| 270^{\circ} | \frac{3\pi}{2} | (0, -1) |
| 360^{\circ} | 2\pi | (1, 0) |
Memorization Tip
To quickly recall coordinates, remember:
- Cosine is the x-coordinate.
- Sine is the y-coordinate.
Trigonometric Functions on the Unit Circle
Sine and Cosine
The sine and cosine functions are derived from the circle as follows:
- \cos(\theta) = x
- \sin(\theta) = y
For example, at \theta = 90^{\circ}:
- \cos(90^{\circ}) = 0
- \sin(90^{\circ}) = 1
Tangent
The tangent function relates sine and cosine:
- \tan(\theta) = \frac{\sin(\theta)}{\cos(\theta)}
Reciprocal Functions
Other functions include cosecant, secant, and cotangent:
- \csc(\theta) = \frac{1}{\sin(\theta)}
- \sec(\theta) = \frac{1}{\cos(\theta)}
- \cot(\theta) = \frac{1}{\tan(\theta)}
Cheat Sheet: Unit Circle Values
Common Angles
Here’s a quick reference table for the most frequently used angles:
| \theta (Degrees) | Radians | \sin(\theta) | \cos(\theta) | \tan(\theta) |
| 0^{\circ} | 0 | 0 | 1 | 0 |
| 30^{\circ} | \frac{\pi}{6} | \frac{1}{2} | \frac{\sqrt{3}}{2} | \frac{\sqrt{3}}{3} |
| 45^{\circ} | \frac{\pi}{4} | \frac{\sqrt{2}}{2} | \frac{\sqrt{2}}{2} | 1 |
| 60^{\circ} | \frac{\pi}{3} | \frac{\sqrt{3}}{2} | \frac{1}{2} | \sqrt{3} |
| 90^{\circ} | \frac{\pi}{2} | 1 | 0 | Undefined |
Applications of the Unit Circle
Real-Life Examples
- Waves and Oscillations: The unit circle describes periodic phenomena like sound and light.
- Rotational Motion: Engineers use it to model gears and wheels.
- Digital Signals: In computer science, it aids in signal processing.
Problem-Solving Techniques
- Angle Conversion: To switch between radians and degrees:
- \text{Degrees to Radians: } \theta \times \frac{\pi}{180}
- \text{Radians to Degrees: } \theta \times \frac{180}{\pi}
Step-by-Step Problem Solving Using the Unit Circle
Problem 1: Find the Sine and Cosine of \theta = 45^{\circ}
Step 1: Convert the angle to radians if necessary.
\theta = 45^{\circ} = \frac{\pi}{4}Step 2: Recall the coordinates of \frac{\pi}{4} on the unit circle.
Coordinates: \left(\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2}\right)
Step 3: Identify sine and cosine.
\sin(\theta) = \frac{\sqrt{2}}{2}\cos(\theta) = \frac{\sqrt{2}}{2}Problem 2: Find \tan(60^{\circ})
Step 1: Convert the angle to radians if necessary.
\theta = 60^{\circ} = \frac{\pi}{3}Step 2: Recall the coordinates of \frac{\pi}{3} on the unit circle.
Coordinates: \left(\frac{1}{2}, \frac{\sqrt{3}}{2}\right)
Step 3: Use the tangent formula.
\tan(\theta) = \frac{\sin(\theta)}{\cos(\theta)} = \frac{\frac{\sqrt{3}}{2}}{\frac{1}{2}} = \sqrt{3}Answer: \tan(60^{\circ}) = \sqrt{3}
Problem 3: Find \sin(\theta) for \theta = 210^{\circ}
Step 1: Convert the angle to radians.
\theta = 210^{\circ} = \frac{7\pi}{6}Step 2: Locate the angle in the correct quadrant.\frac{7\pi}{6} is in Quadrant III.
Step 3: Use symmetry and recall coordinates.
Reference angle: 30^{\circ} = \frac{\pi}{6}
Coordinates in Quadrant III: \left(-\frac{\sqrt{3}}{2}, -\frac{1}{2}\right)
Step 4: Identify sine.
\sin(\theta) = -\frac{1}{2}Answer: \sin(210^{\circ}) = -\frac{1}{2}
Unit Circle Common Mistakes and How to Avoid Them
Mistaking Signs
Always check the quadrant to determine the correct signs for sin\sinsin and cos\coscos.
Forgetting Radian Measures
Familiarize yourself with common radian values. Use flashcards if needed.
Overlooking Special Triangles
Special triangles are the key to unlocking trigonometric values quickly.
FAQ
Focus on the symmetry of the circle. Memorize the first quadrant, then use it to deduce values in other quadrants.
It simplifies calculations and provides a visual representation of trigonometric functions.
Use \cos(\theta) for the x-coordinate and \sin(\theta) for the y-coordinate.
Degrees divide a circle into 360 parts, while radians measure the angle as the length of the arc divided by the radius.