Trigonometry is one of the main topics of IB Maths and a fascinating branch of mathematics that helps us understand relationships between the angles and sides of triangles. Two fundamental tools in this journey are the Sin Rule and the Cos Rule. These rules can seem a bit intimidating at first, but with clear explanations and practical examples, they become easy to grasp. Let’s break these concepts down step-by-step and explore their applications in real-world problems.
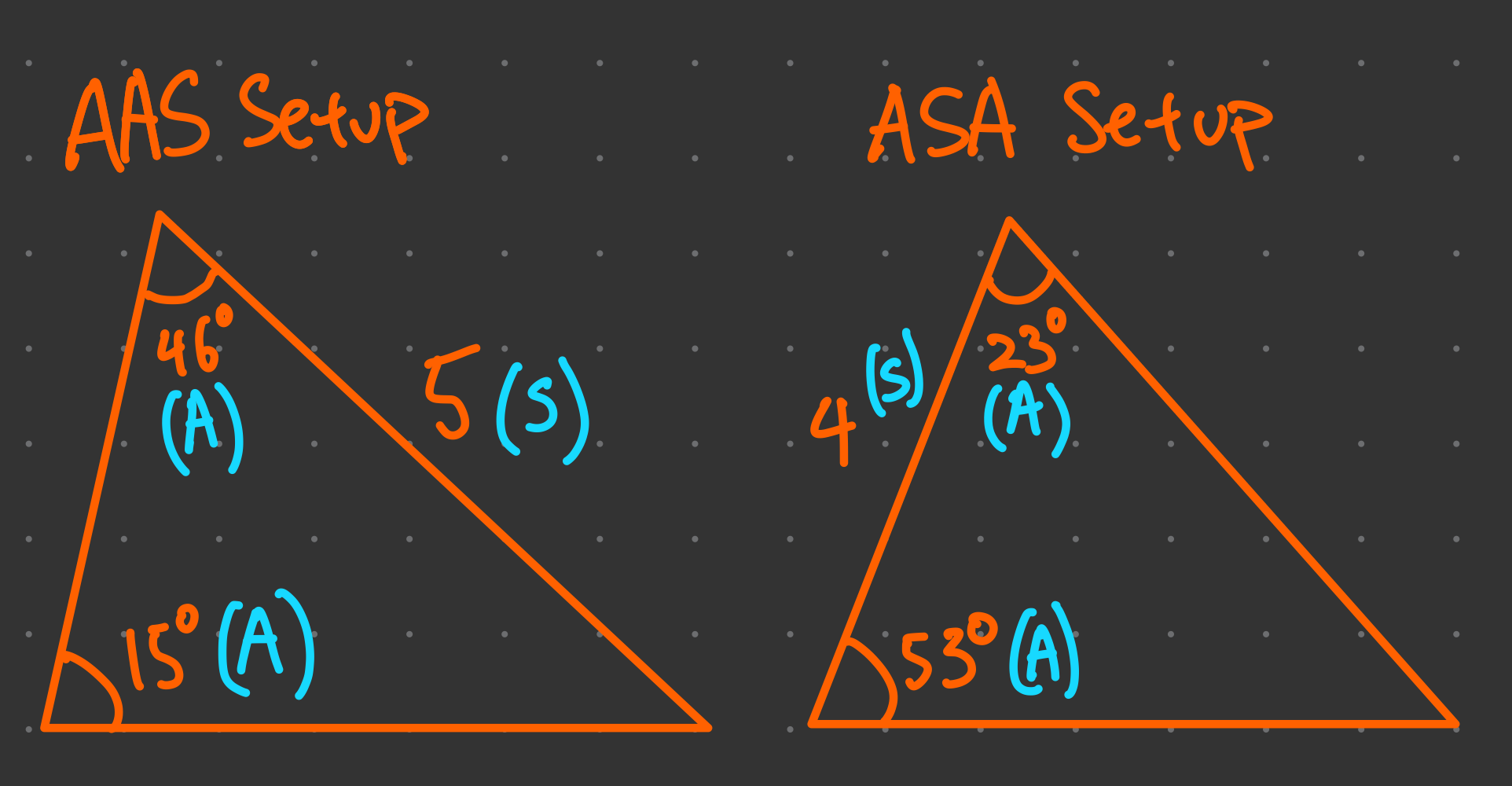
What is the Sin Rule?
The Sin Rule (or Sine Rule) is a formula used to relate the sides and angles of a triangle. This rule is especially helpful when dealing with non-right triangles, also known as oblique triangles. The Sin Rule states:
\frac{a}{\sin(A)} = \frac{b}{\sin(B)} = \frac{c}{\sin(C)}Here:
a, b, and c are the sides of the triangle.
A, B, and C are the angles opposite these sides.
In essence, the ratio of a side to the sine of its opposite angle remains constant throughout the triangle.
When Do You Use the Sin Rule?
The Sin Rule is applicable in the following scenarios:
When you know two angles and one side (AAS or ASA).
When you know two sides and a non-included angle (SSA).
Example: Using the Sin Rule
Imagine a triangular park where:
One side measures 50 meters.
The angles opposite this side and another side are 30° and 45°, respectively.
We want to find the length of the other side.
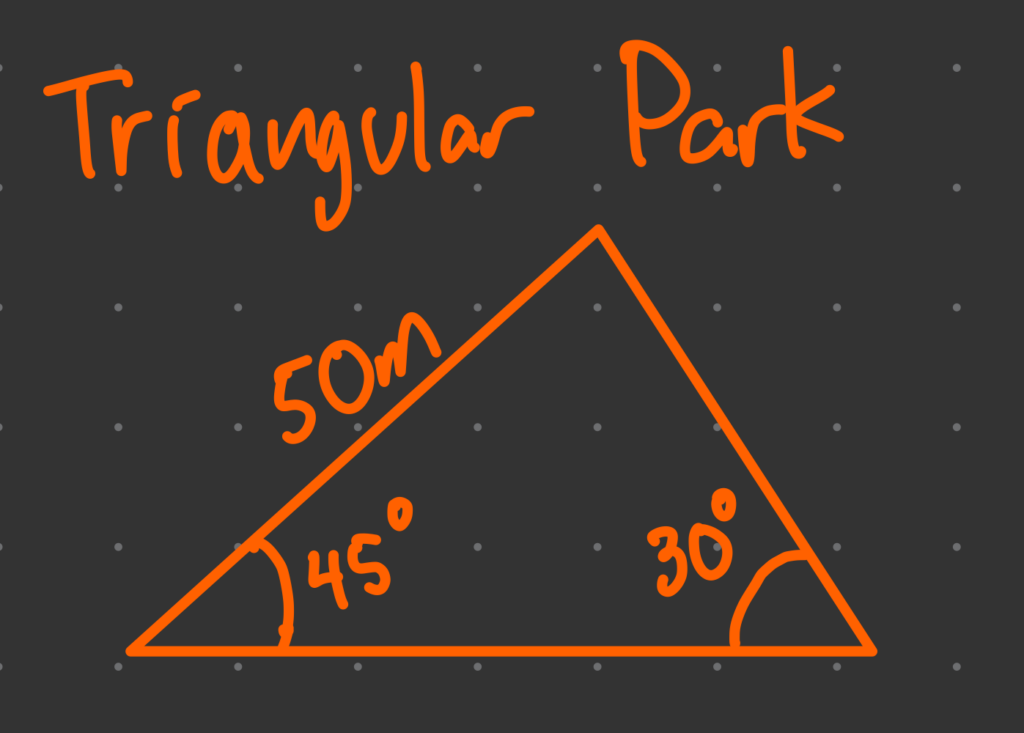
Step 1: Write the Formula
\frac{a}{\sin(A)} = \frac{b}{\sin(B)}Step 2: Plug in Known Values
Let the side we’re solving for be b. \frac{50}{\sin(30^\circ)} = \frac{b}{\sin(45^\circ)}
Step 3: Solve for b
b = \frac{50 \cdot \sin(45^\circ)}{\sin(30^\circ)}Using approximate values:
\sin(30^\circ) = 0.5 \sin(45^\circ) = 0.707 b = \frac{50 \cdot 0.707}{0.5} = 70.7 \text{meters}What is the Cos Rule?
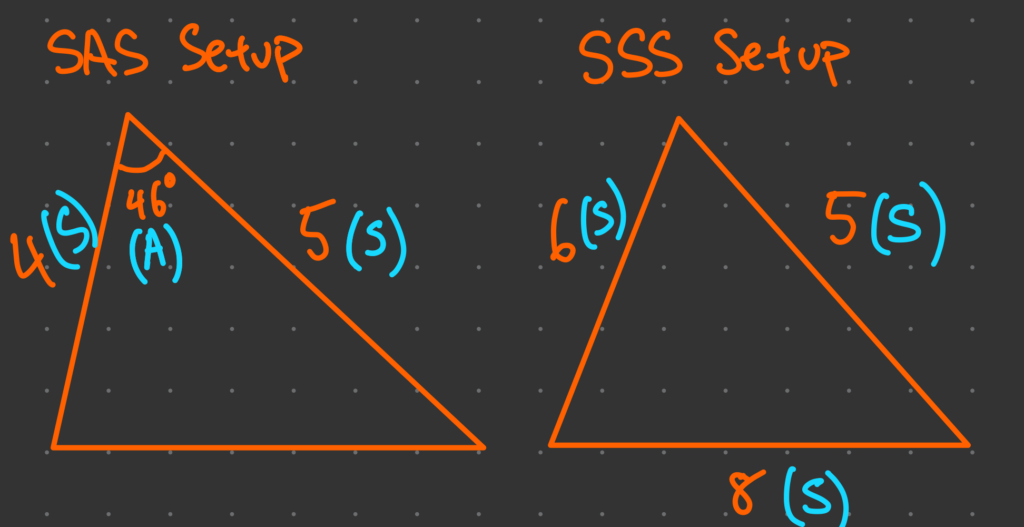
The Cos Rule (or Cosine Rule) is another powerful tool for solving triangles. It relates the lengths of all three sides of a triangle to the cosine of one of its angles. The formula is:
c^2 = a^2 + b^2 – 2ab \cdot \cos(C)
Here:
a, b, and c are the sides of the triangle.
C is the angle opposite side c.
This rule is particularly helpful for:
Finding the length of a side when you know two sides and the included angle (SAS).
Finding an angle when you know all three sides (SSS).
Example: Using the Cos Rule
Suppose you’re measuring the distance between two points across a lake. The sides of the triangle are:
a = 80 meters
b = 60 meters
The included angle C = 120°
We want to calculate the third side, c.
Step 1: Write the Formula
c^2 = a^2 + b^2 – 2ab \cdot \cos(C)Step 2: Plug in Known Values
c^2 = 80^2 + 60^2 – 2 \cdot 80 \cdot 60 \cdot \cos(120^\circ)Note: \cos(120^\circ) = -0.5
c^2 = 6400 + 3600 – 2 \cdot 80 \cdot 60 \cdot (-0.5) c^2 = 6400 + 3600 + 4800 = 14800 c = \sqrt{14800} \approx 121.5 \text{meters}Comparing the Sin Rule and Cos Rule
Both rules are essential tools for solving triangles, but they serve different purposes:
| Aspect | Sin Rule | Cos Rule |
|---|---|---|
| Applies to | Angles and opposite sides | Angles and any sides |
| Best for | Non-right triangles, AAS or SSA cases | SAS or SSS cases |
| Complexity | Simple ratios | Slightly more computation-intensive |
Real-World Applications
1. Navigation
Both rules are indispensable in navigation. For instance, sailors use them to calculate distances and angles when plotting courses.
2. Architecture
Architects use these rules to design structures where precise angles and lengths are necessary, such as in bridges or roof designs.
3. Astronomy
In astronomy, the Sin and Cos Rules help determine distances between celestial objects by forming virtual triangles in space.
4. Engineering
Civil engineers rely on these rules to calculate forces in structures like cranes, beams, and trusses.
Summary
Understanding the Sin Rule and Cos Rule is crucial for solving a wide variety of mathematical and real-world problems. The Sin Rule links sides and angles in proportional relationships, while the Cos Rule provides a way to calculate unknown sides and angles when dealing with more complex setups.
FAQ
Yes, but right triangles are usually solved with simpler trigonometric ratios like \sin\theta, \cos\theta, \tan\theta These rules shine in non-right triangles.
Using the Sin Rule incorrectly, such as matching the wrong side and angle, will lead to incorrect results. Always double-check that you’re pairing the correct side with its opposite angle.
Use the Sin Rule if you have angles and their opposite sides.
Use the Cos Rule if you have two sides and the included angle or all three sides.
These rules apply to 2D triangles. For 3D shapes, extended principles in vector mathematics or spherical trigonometry might be required.
